レバレッジETFは減価リスクがあるから危険と言われることがあります。
超簡単な例でいうと、株式指数が10%上昇し翌日10%下落した場合:
レバなし:1.1 x0.9= 0.99
3倍レバレッジ:1.3 x0.7=0.91
つまりレバなしであれば合計1%の下落で済むにも関わらず、3倍レバレッジであれば合計9%も下落する。
このような上昇と下落をどんどん繰り返せば、レバレッジ3倍ETFはどんどん下落していくので危ないと。
金融庁のレバレッジETF注意喚起にも似たようなことが書いてあります。
中長期の期間をとった場合、一般的に株価は①や②のように上下動を繰り返すことが多く、③や④のように一方向に上昇又は下落が続くケースは少ないと考えられます。
確かに株価が上下動を繰り返せば、レバなしよりも3倍レバの方が下落が大きくなる「減価リスク」が顕在化します。これは間違っていません。
問題は、上下動を繰り返す相場が本当に起きやすいのか?という点です。
上下動相場というのは、様々なパターンのうちの一つのシナリオに過ぎません。減価リスクが語られるとき、そのシナリオの発生確率が完全に見過ごされていると思います。
定量的に考えてみます。例えばS&P500のリスク・リターンは20%・7%です。(年率で考えてます。)
株価変動を幾何ブラウン運動でモデル化すると、上昇する確率は66%、下落する確率は34%です。
つまり、そもそも指数(S&P500)は上昇確率が下落確率より高いにも関わらず、より発生しにくいシナリオである上下動相場を持ってきて、減価リスク云々語るのはなんだか変だということ。
ざっくり言えば、上昇確率 > 下落確率なのだから上昇を続ける相場の方が発生しやすいので、その場合はレバレッジありの方が断然有利になります。
結局何が言いたいかというと、
レバレッジETFの減価リスクの話は、特定の相場を切り抜いて語られているだけで、そもそもの指数の特性「上昇確率 > 下落確率」が置き去りにされてるってことです。
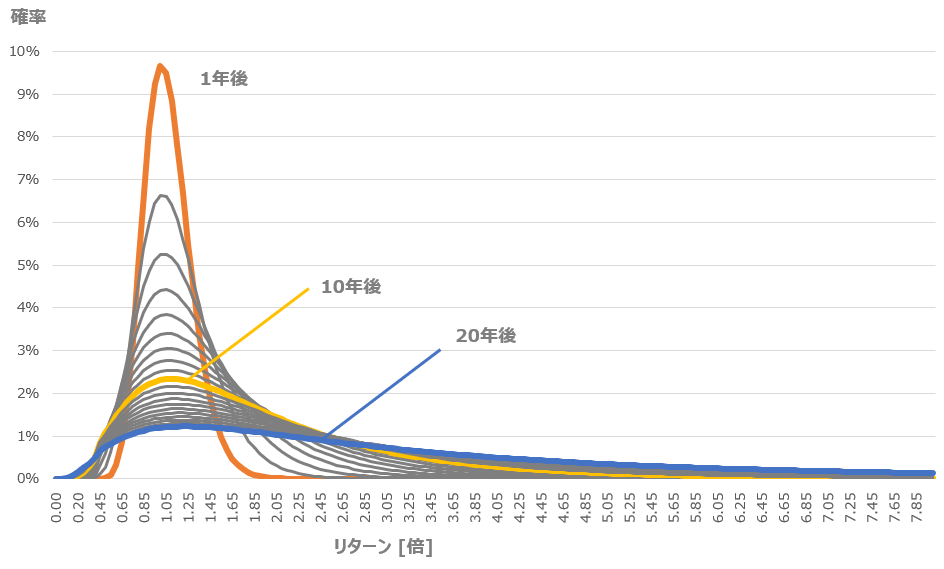
一方で、レバレッジETFの挙動を確率分布で分析すれば、そのようなシナリオ切り抜きの弊害はなくなります。
なぜなら、確率分布をつかえば全てのシナリオを包括してトータルリターンや元本割れ確率を計算することができるからです。(※)
確率分布を用いた分析例は、たとえばコレ。
※ただし暴落の効果を取り入れるには少し数学的テクニックが必要です。以下記事を参照。
記事が役に立ったらクリックお願いします↓